Tarea

Las modernas transmisiones automáticas controladas electrónicamente ya no tienen un interruptor selector de potencia/economía. La unidad de control usa los sensores disponibles para determinar si el conductor preferiría conducir en el área de desempeño o economía. Pero, ¿cómo decide el controlador? Un pasajero probablemente podría juzgar más bien, después de cierta distancia, si es conducido poderoso o económico. Transferir las reglas del pensamiento humano a la computadora es la tarea de la lógica difusa.

Función

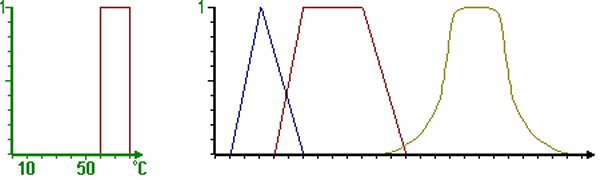
La palabra fuzzy significa algo así como "borde difuso". Esto se remonta a causa del Sr. Lotfi A. Zadeh, el que la desarrolló en los años 80 del siglo pasado en la Universidad de Berkley. El diagrama verde muestra sobre el ejemplo de la temperatura, como era hasta entonces. Todas las temperaturas entre 60° y 80° C se podían asignar sólo con los términos "frío" o "caliente". Exactamente ahí se encuentra el problema. ¿Se debe excluir una temperatura de 59,5° C? Tales saltos solo capturan la realidad probablemente de manera insuficiente. ¿Y cómo se puede evaluar ahí la posición del pedal del acelerador?

Por eso la lógica difusa establece una variable de pertenencia (valor entre '0' y '1'). Con ello se asociaría la temperatura de 59,5° C, por una determinada función de pertenencia de rango "muy caliente" y sobre otra función de pertenencia de rango "caliente". El diagrama negro (a la derecha) muestra a esto varias dependencias. La pertenencia se muestra por regla en forma de un triángulo (azul), un trapecio (rojo) o una distribución normal (marrón). Entre ambos resultan intersecciones a las que se aplican los valores del eje X, que tanto en uno como en el otro rango se suelen asignar con un diferente valor de pertenencia. Con el trapezoidal se alcanza entonces en el medio un cierto rango-X de valor 1 como resultado de pertenencia.

En nuestro ejemplo del selector, se asignan ciertas posiciones del pedal del acelerador con diferentes valores de pertenencia a ciertos rangos (poca aceleración, algo más de aceleración, etc.). Del mismo modo se toman otras variables, tales como la velocidad, con la que se pisa el pedal del acelerador. Al final se compensan las diferentes variables con sus valores de pertenencia entre ellas, y sale a pesar de ser valores 'difusos' un resultado igual de claro, la potencia o la economía. 06/09