 Mathematik - Funktionen 3 Mathematik - Funktionen 3

In den vorigen Kapiteln haben wir den Unterschied zwischen einer Funktion mit Funktionsvorschrift und einer
grafischen Darstellung von Messwerten erklärt. Letztere werden z.B. mit so einem oben gezeigten Gerät
ermittelt, um im Falle von zu schnellem Fahren Bußgeld eintreiben zu können.
Angefangen hat das mit der Aufnahme der Zeit beim Durchfahren einer gewissen Strecke. War die Zeit
unterhalb eines Limits, dann war auch hier Bußgeld fällig. Im letzten Fall wurde eine
Durchschnittsgeschwindigkeit über eine gewisse Strecke ermittelt, bei der Anlage oben im Prinzip die
Geschwindigkeit an einem gewissen Punkt.
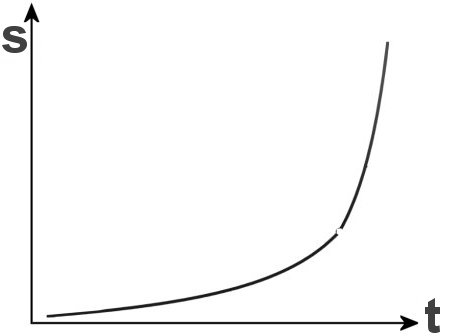
Und genau dazu wird die sogenannte 'Ableitung' verwendet. Es wäre die Steigung einer Tangente an dem
eingezeichneten Punkt. Sie haben so eine Gerade schon im Kapitel Funktionen 1 kennengelernt:
| f(x) = 2x | f(x) = 3x |
f(x) = 4x |
Dort wurde Ihnen erklärt, dass der Multiplikator von x die Steigung einer Geraden ergibt. Bei f(x) = 2x steigt das f(x)
langsamer als bei f(x) = 4x. Und da die Steigung im Diagramm oben Δs/Δt
ist, entspricht sie exakt der Geschwindigkeit:
| | Δs |
| v | = |  |
| | Δt |
Unten einmal das Diagramm. Von dem Punkt aus, bei dem wir die Geschwindigkeit bzw. Steigung bestimmen
wollen, gehen wir um Δt weiter und erhalten eine um Δs verlängerte Strecke, die
zurückgelegt wurde. Die Durchschnittsgeschwindigkeit auf dieser Strecke wird durch die Gerade 1 dargestellt.
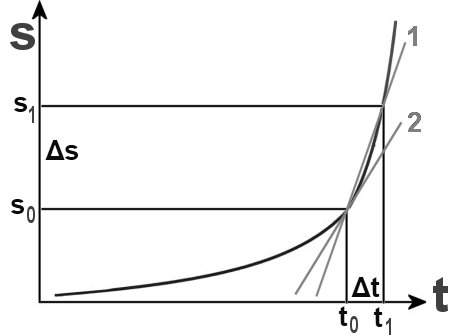
Bei der Bildung einer Ableitung kommt es darauf an, t1 jetzt langsam auf t0
zurückzuführen, also Δt Null werden zu lassen. Dadurch wird die Gerade 1 langsam zur
Geraden 2, was dann eine Tangente an die Kurve exakt im Punkt t0 wäre. Wir schreiben das so:
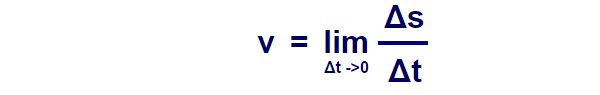
Wenn man also einen unendlich kleinen Bereich an dem Punkt S0 und t0 der obigen Funktion betrachtet, kann man den Anstieg als linear annehmen und von diesem linearen
Anteil hat die Differentialrechnung ihren Namen. Man geht hier aus von einer Differenz, oben z.B. von t1 - t0, die man immer kleiner werden lässt.
Wir sind also jetzt von der durchschnittlichen zur momentanen Geschwindigkeit gekommen. Geometrisch hat sich die Sekante, also eine Verbindung zweier Punkte eines Kreisbogens, in eine Tangente
gewandelt, mit also nur noch einem Berührpunkt, exakt dem, für den wir unsere Geschwindigkeit brauchen.
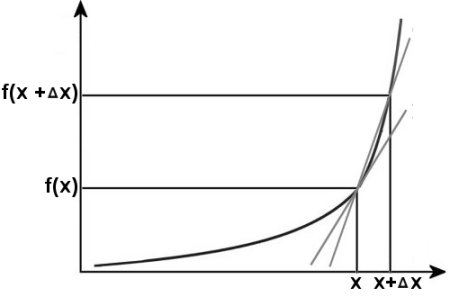
Wenn Sie dieses Bild mit dem vorigen vergleichen, könnten Sie meinen, es sei das gleiche nur mit einer anderen Beschriftung. Stimmt. Und doch soll es hier ausdrücken, dass es sich um eine Funktion
handelt. Eine Kurve, die aus Messwerten gebildet wird, besteht eigentlich nur aus ein paar Stützstellen, die durch eine Linie verbunden werden.
Eine Funktion hingegen ist in jedem Punkt der Kurve exakt definiert. Und nur hier kann ich natürlich langsam vom Punkt f(x +Δx) / x +Δx auf f(x) / x zubewegen also Δx gegen Null gehen lassen:
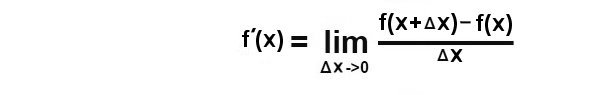
|